Self Learning Machines for the Multiplication of 2 numbers [Part 1]

01 May 2016

Challenge the “Mighty” computers

Back in the 90’s when I was a kid I clocked 0.05sec for multiplying two numbers for which I won the national award. I was faster than the so called powerful computers at that time;). I still hold the record for the same. People say that these days computers are much powerful and can do computations trillion times faster than us. So I decided to challenge these “Mighty” computers. This is the battle that has waited for decades. Many maestros are predicting that this is the battle of the century.

Lets set the competition rules right.

result = a * b
Given the "result" and "a" , Find "b".

For example:
result=20
a=5
b=?

I know that the computers are smart. Unfortunately we are not supposed to use addition/division to solve this.

Note: Addition/Substraction/Division cannot be used. example: b= result/a; is not allowed

Since the computers are programmed I would know if the computer broke any of the above rules.Unfortunately for the computer/anyone for that matter would not know even if I break the law since they cannot peak into my brain and figure out the algorithm. How can a computer solve this? It is not supposed to do repititive addition or division to find out the answer.A friend of mine is a decent programmer. He is gonna make the computer solve this.

Random gi TADA!!!! Computers are fast in doing a particular operation. So my friend decided to use the random number generatin method to solve this.

Repeatedly generate random numbers to find out for what value of “b” the result is 20.

begin
a=5
repeat untill result=20
    b=random()
    result=a*b;
    if result == 20
    print "BRAVO"
        break;
end

I beat the computer hands down!!

The above results were no where close to my record. The computer repeatedly generated random numbers, Even if it is multi threaded or distributed across multiple compute nodes, It was no where close to beating me.I beat the computer hands down.

I could see the dys and the dxs.

My friend is not happy with the results.He started scrambling something on his notebook. I got a little curious. He did a litle math in his book and I could see his sparkling eyes beaming with confidence.I could see the dys and the dxs. I could smell something was fishy.He started explaining what he was upto with these computation graphs.

The power of calculus

Before we dive in, lets just take step back try to understand what is gradient? In plain English, What is the effect of input on output? Lets take a very simple example of multiplication.

read as “The effect of input ‘a’ on function ‘*‘ ”

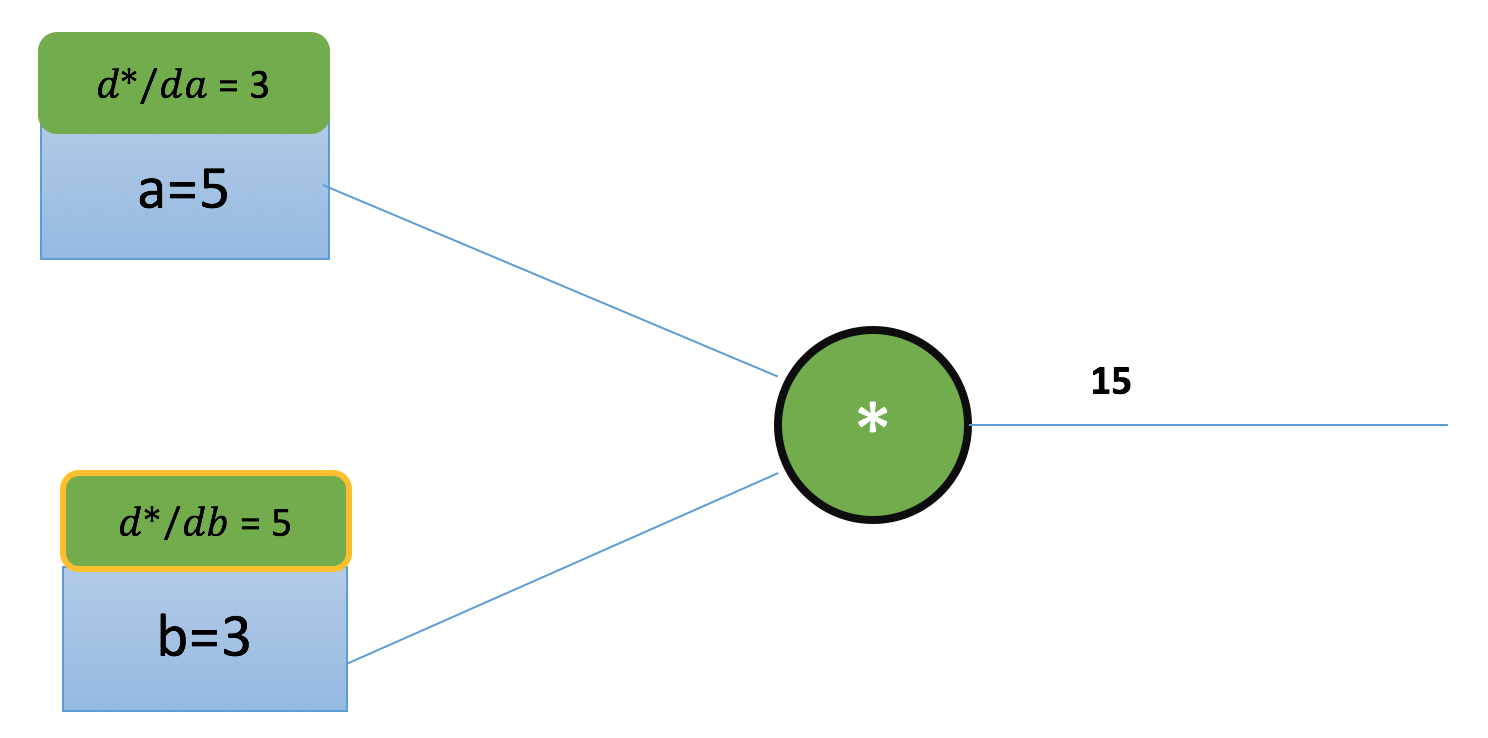
The green box indicates the derivative aka the effect of input ‘a’ on *.

Intuitively what this means is if you increase the value of input ‘a’ by 1 unit, it is going to increase the output by 3 units(positive influence). For example if you increase the value of a to 6 from 5, the output is increased by 3 units to 18.

Another example, Lets take another example of subtraction.

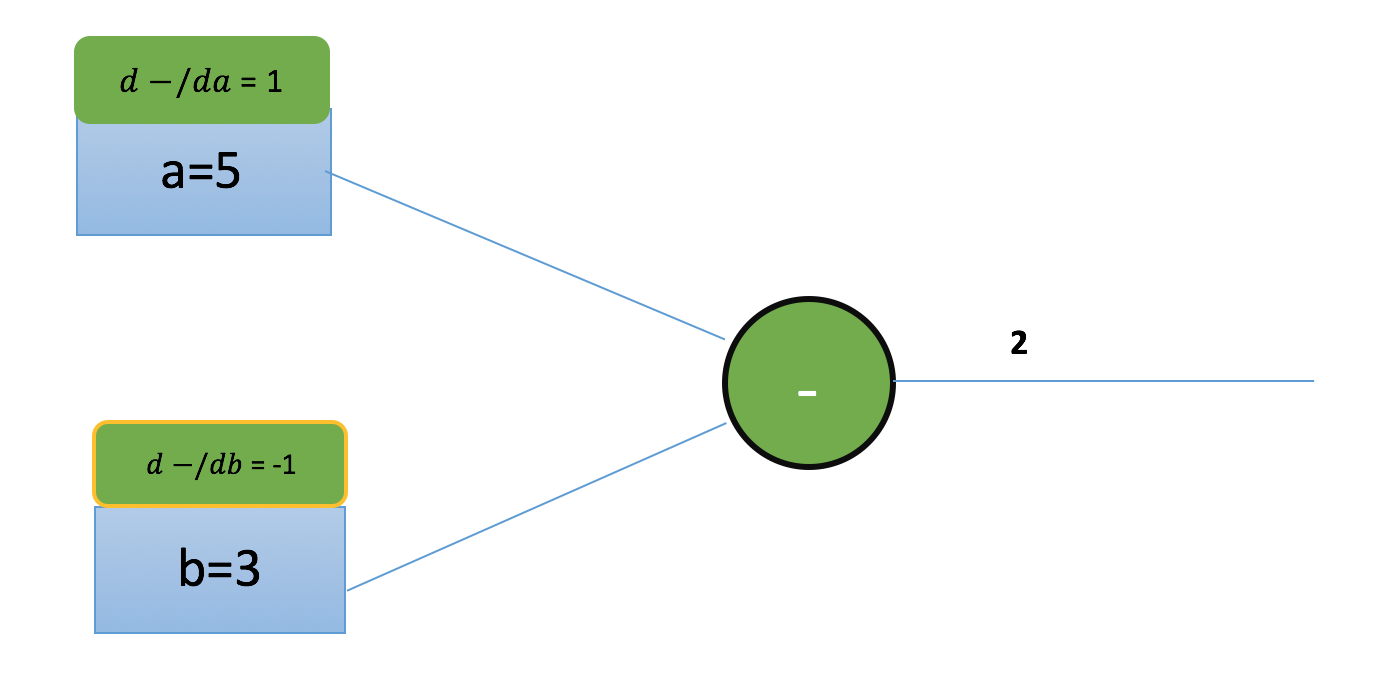
Lets analyze the effect of input ‘b’ on function ‘-’ . The negative gradient indicates the negative influence , meaning increasing the input b will reduce the output. For example if you increase the input b by 1 unit say b = 4 , the output is reduced by 1 unit i.e . output = 1.

This is just getting better and better

Lets get back to the man vs the machines battle. Does the following computation graph aka function chain aka multiplication followed by subtraction ;) ring any bells?

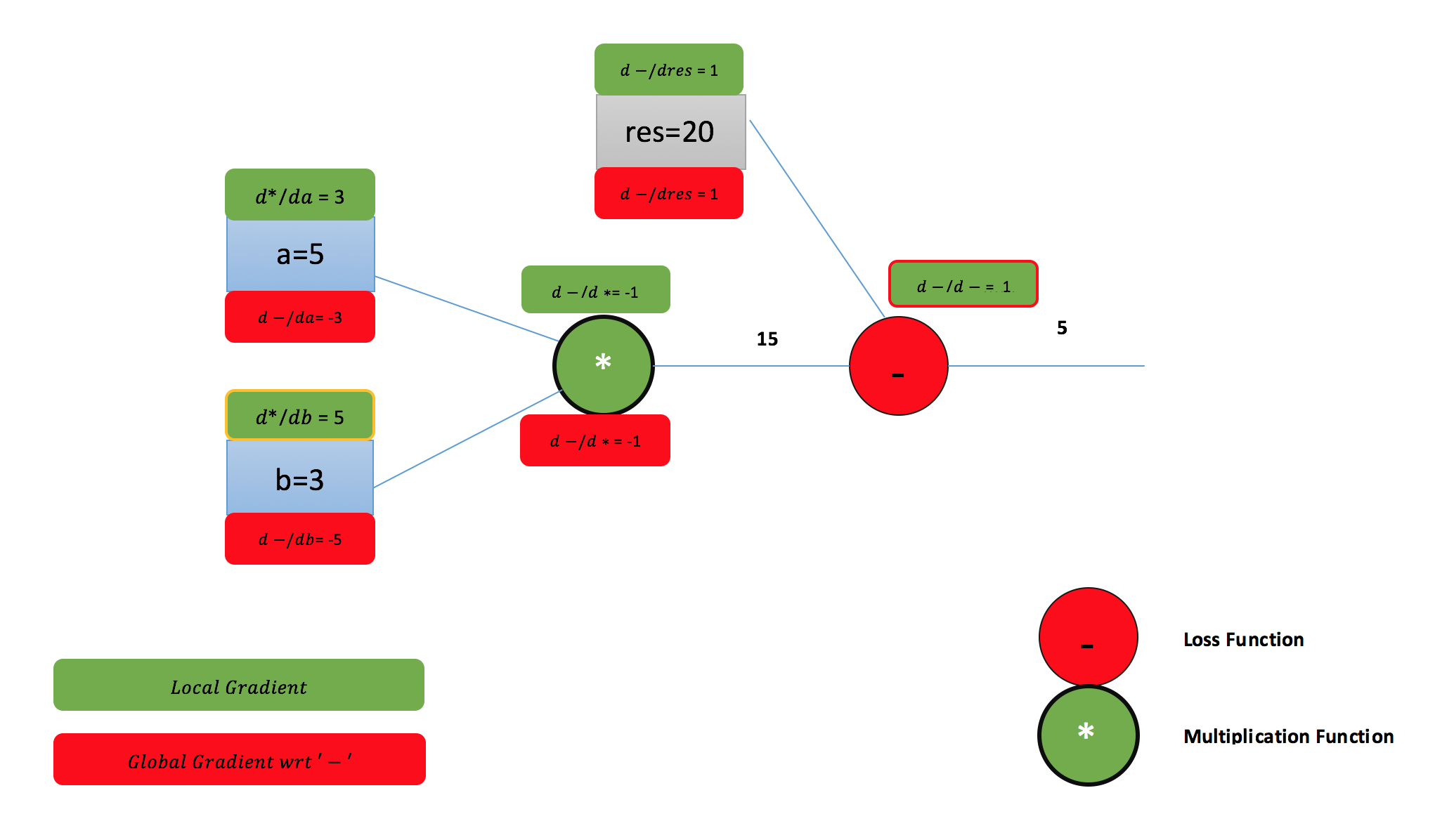
Nothing fancy. The same old story of “The effect of input on output”. Notice the red colored boxes (= -3). In plain English “The effect of input ‘a’ on function ‘–‘ (minus) ”. For example: = -5

If you increase the input b by 1 unit the output will decrease by 5 units(negative influence).

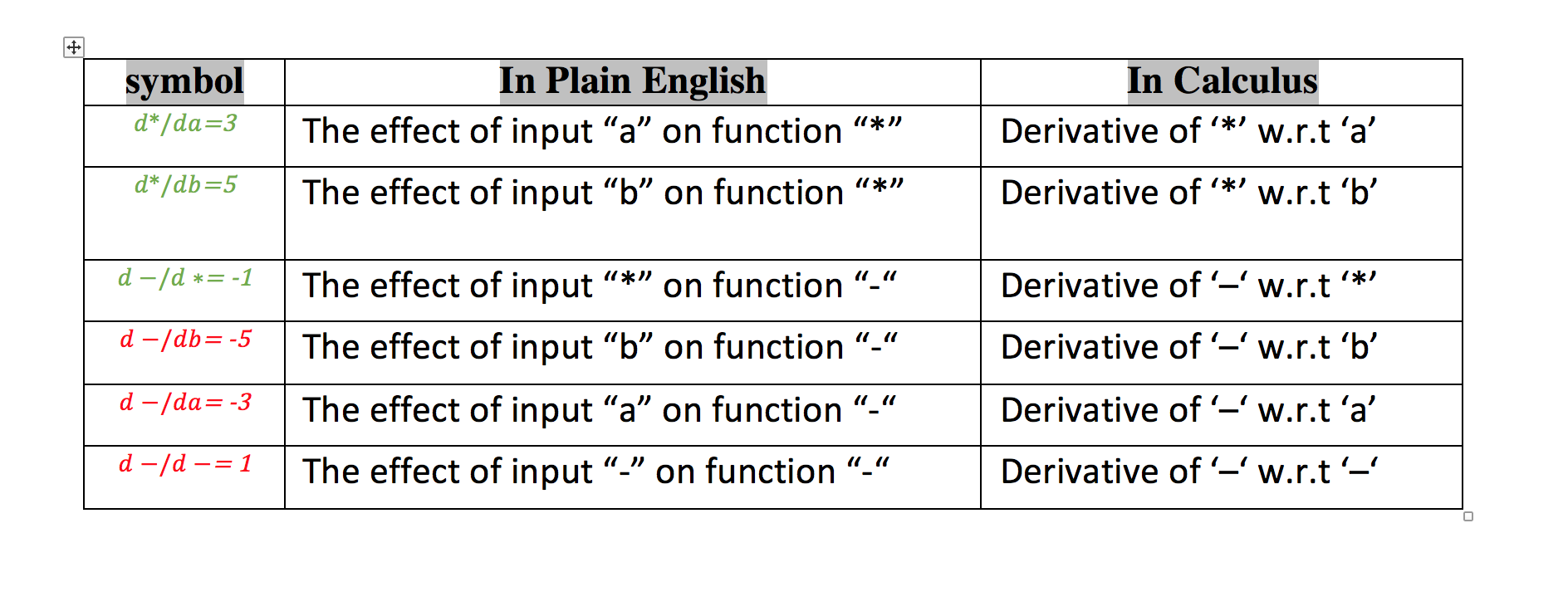
The red colored minus function is our loss function which determines how well we chose the value for b. Given: a=5 b=? res=20

Lets start with a some random number 3 for “b”. (I assumed a close number to make the math easy).

a=5
b=3
res=15
loss=5

newb = b – (learningRate * )

Note: learning rate controls the pace at which we want to get to the optimal solution. learningRate=0.01 (having a small learning rate is good. Remember Slow and steady wins the race)

newb = 3 – (0.01 * -5)
newb = 3 – (-0.05)
newb = 3 + 0.05
newb = 3.05

a=5
b=3.05
res=15.25
loss=4.75

We repeat the above step till we get the loss 0.

newb = 3 .05– (0.01 * -5)
newb = 3.05 – (-0.05)
newb = 3.05 + 0.05
newb = 3.10

a=5
b=3.10
res=15.50
loss=4.50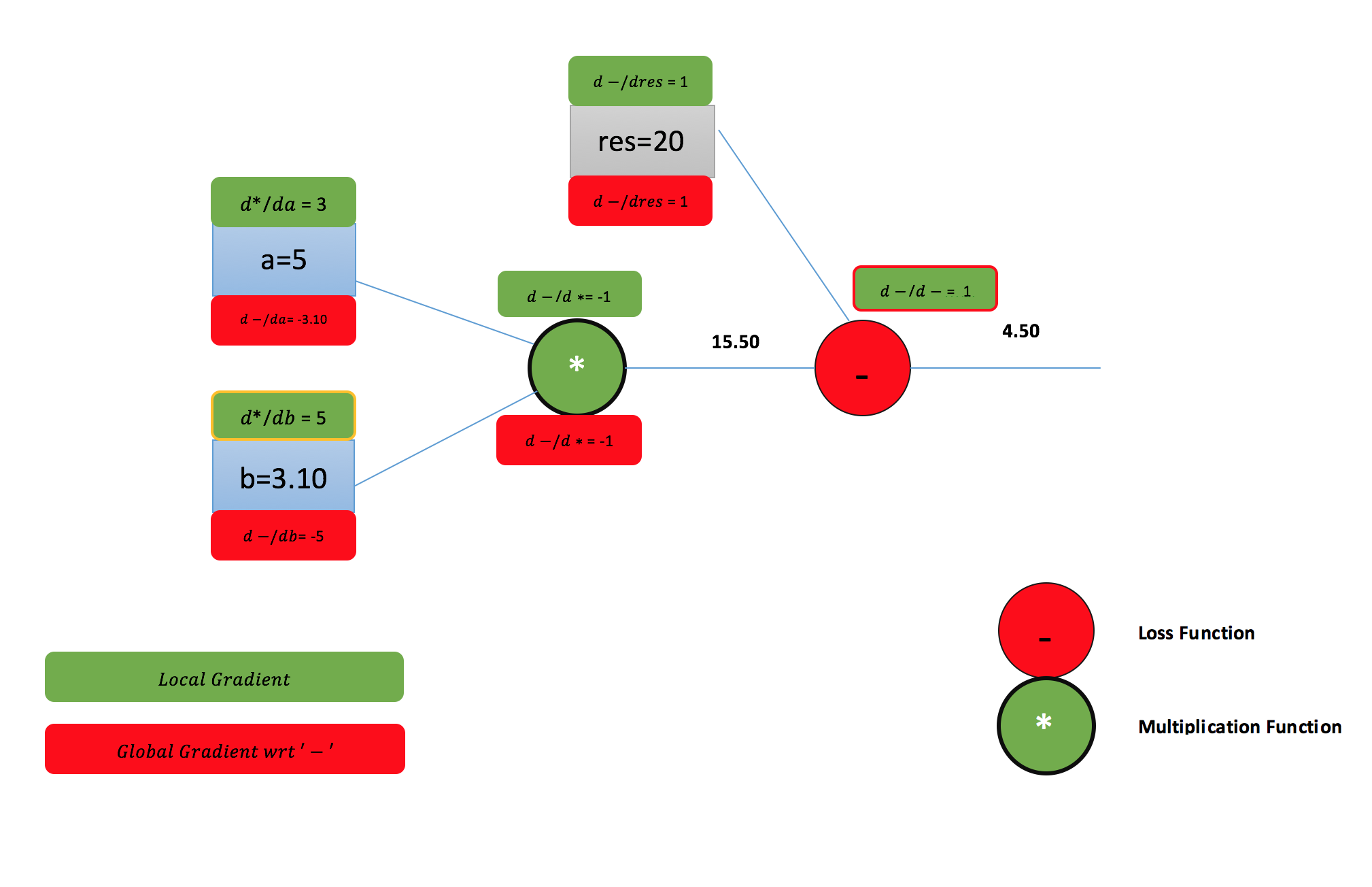

Notice the loss function value which is getting reduced every iteration. After a few number of iteration We arrive at the optimal solution.

a=5 b=4 res=20 loss=0

Pick-and-shovel if the numbers are changed.

Looks like the computer has found a method which looks efficient(which is still debatable). I might definitely beat the machine for the above example. But I might have to Pick-and-shovel if the numbers are changed. The same approach can yield better results if implemented efficiently and using some better update methods.